在本示例中,我们考虑将单个光子发射器耦合到光纤中。 有关系统和数值方法的详细信息,请参见参考文献[1]。
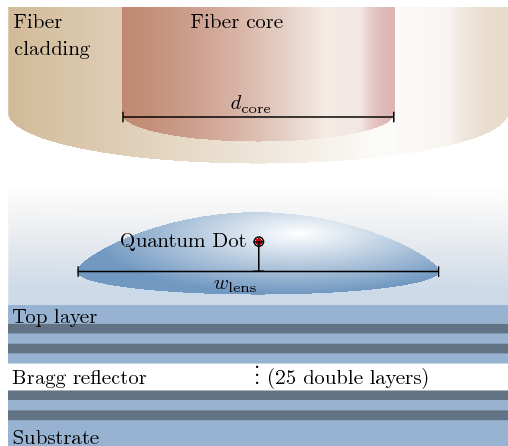
单光子源由一个嵌入在砷化镓(GaAs)中制成的球形微透镜中的量子点(QD)组成。底层的布拉格多层结构将量子点发出的光反射回上半球。光被耦合到量子点上方的光纤中,该光纤由均匀的光纤芯和光纤包层组成(见下图)。
计算利用了设置的径向对称性。 因此,透镜的形状可以通过文件 layout.jcm 中定义的扇形和平行四边形之间的布尔交集来创建。
对于光纤模式计算,可以从文件fiber_modes/layout.jcm中的完整系统布局中提取光纤横截面的几何形状。
耦合效率的确定分三步进行:
1. 首先,确定光纤的传播模式;
2. 接下来,必须模拟量子点发射的场。 与微透镜内的波长相比,量子点的延伸相对较小。 因此可以将其建模为类点状偶极源;
3. 最后,确定传播光纤模式和发射场之间的重叠积分。 耦合效率由重叠量除以偶极子发射的总功率得到。 偶极子发射和重叠积分可以通过文件 project.jcmp 中定义的两个后处理偶极发射和模态重叠获得:
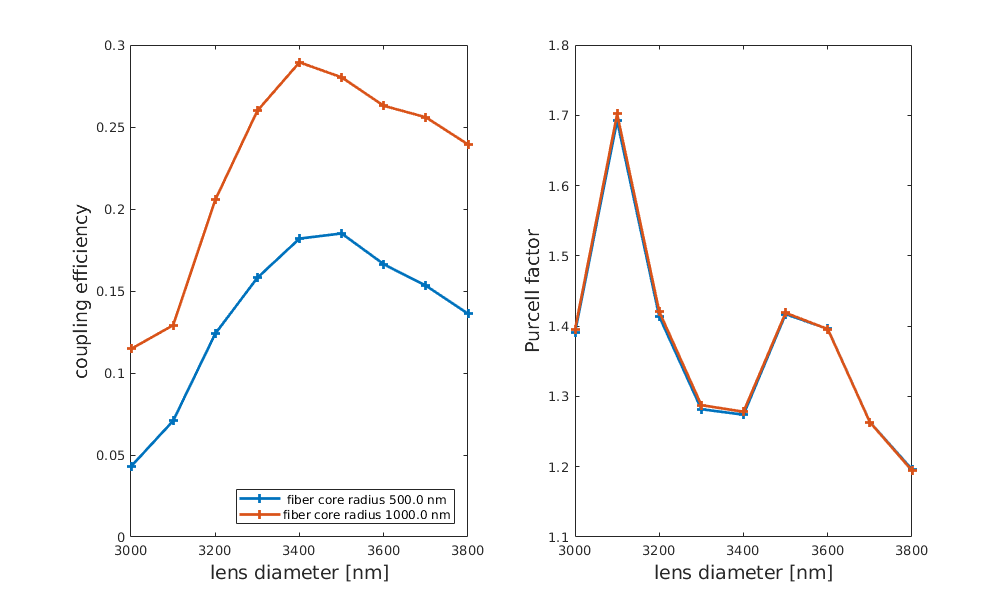
下图显示了对基本光纤模式和珀塞尔系数 [*] 作为透镜直径 和光纤芯直径 的函数的耦合效率的扫描。
参考文献:
[*] The Purcell factor is the quotient between the dipole emission in the structure and the emission of a dipole in a homogeneous space with the background material at the dipole position.
[1] P.-I. Schneider, et al., Numerical optimization of the extraction efficiency of a quantum-dot based single-photon emitter into a single-mode fiber. Optics Express 26, 8479 (2018). https://doi.org/10.1364/OE.26.008479
|