利用光学手性和内置手性参量的形式,可以在JCMsuite中计算光学散射体的手性响应。结果表明,时间谐波光学手性密度服从局部连续性方程[1]。这使得手性行为的分析类似于电磁能量的研究。
圆偏振平面波是光手性的本征态。因此,近场光手性密度与圆偏振密切相关。在几何光学中,四分之一波板将线偏振转换为圆偏振是众所周知的。它们是由双折射材料制成的,例如各向异性材料。波片的厚度是寻常(x-)偏振和非寻常(z-)偏振波长差的四分之一。入射平面波在xz方向上线性偏振,在-y方向上传播,如下图所示:
四分之一波片的能量守恒和光学手性
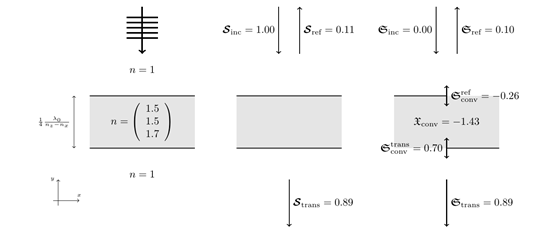
由于线偏振,入射手性通量消失 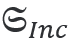 =0。对于一个完美的四分之一波片,反射通量  将消失,而透射手性通量  =1将以圆偏振平面波为单位。从几何光学的角度,我们认为由于波片的各向异性导致了偏振变化或手性转换发生在波片的体积 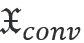 内。对于麦克斯韦方程组的严格解,会产生与这个简化模型的轻微偏差。
在近场中,由于各向异性和材料参数[1]的变化而发生手性转换。利用各向异性电学手性 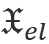 的密度积分,可以在JCMsuite中计算体积贡献。这种转换类似于能量吸收  。对于这个例子中的分段常数材料,界面处的手性转换是通过电磁手性转换通量积分来计算的。它的实部得到 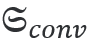 。
最后,通过对界面外域电磁手性通量积分取实数部分给出了反射  和透射  光手性通量。由于光学手性守恒,推导出下式:
适用于任意材料和电磁场。这类似于能量守恒,可写为
光学手性密度 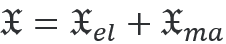 如下所示
研究了四分之一波片近场的光手性密度 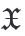  (左)及其体积转换 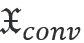 (右)
这是由输出参量:磁性手性密度和各向异性电性手性密度得到的。在这里,目前的符号并没有区分整数(例如  或 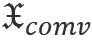 )和密度(例如  )。
注意,各向异性手性密度在计算上比它们的各向同性对应部分更消耗计算资源。由于所涉及的材料是非磁性的(μr=1),计算(各向同性)磁性手性密度就足够了。还需要注意的是,各向异性参量仅适用于具有电场分量或磁场分量的解决方案。这是由于需要对该场进行额外的导数求解。
对四分之一波片近场(见上图)的分析证实了几何光学的预期: 在周围的空气中波片内偏振变化发生 为零(和界面)。向下传播(输出)平面波的光手性密度几乎是圆平面波手性密度的一个单位。发现输出偏振几乎完全圆偏振直至  / 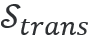 ≈0.9938。通过优化其厚度,可以获得更优异的较低反射性能。
参考文献
[1] (1, 2) Philipp Gutsche, Lisa V. Poulikakos, Martin Hammerschmidt, Sven Burger, and Frank Schmidt. Time-harmonic optical chirality in inhomogeneous space. In SPIE OPTO, Vol.9756, pages 97560X. International Society for Optics and Photonics, 2016.
|


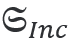 =0。对于一个完美的四分之一波片,反射通量
=0。对于一个完美的四分之一波片,反射通量 将消失,而透射手性通量
将消失,而透射手性通量 =1将以圆偏振平面波为单位。从几何光学的角度,我们认为由于波片的各向异性导致了偏振变化或手性转换发生在波片的体积
=1将以圆偏振平面波为单位。从几何光学的角度,我们认为由于波片的各向异性导致了偏振变化或手性转换发生在波片的体积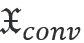 内。对于麦克斯韦方程组的严格解,会产生与这个简化模型的轻微偏差。
内。对于麦克斯韦方程组的严格解,会产生与这个简化模型的轻微偏差。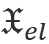 的密度积分,可以在JCMsuite中计算体积贡献。这种转换类似于能量吸收
的密度积分,可以在JCMsuite中计算体积贡献。这种转换类似于能量吸收 。对于这个例子中的分段常数材料,界面处的手性转换是通过电磁手性转换通量积分来计算的。它的实部得到
。对于这个例子中的分段常数材料,界面处的手性转换是通过电磁手性转换通量积分来计算的。它的实部得到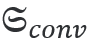 。
。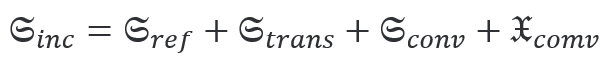
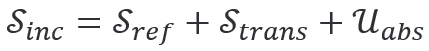
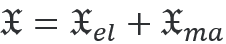 如下所示
如下所示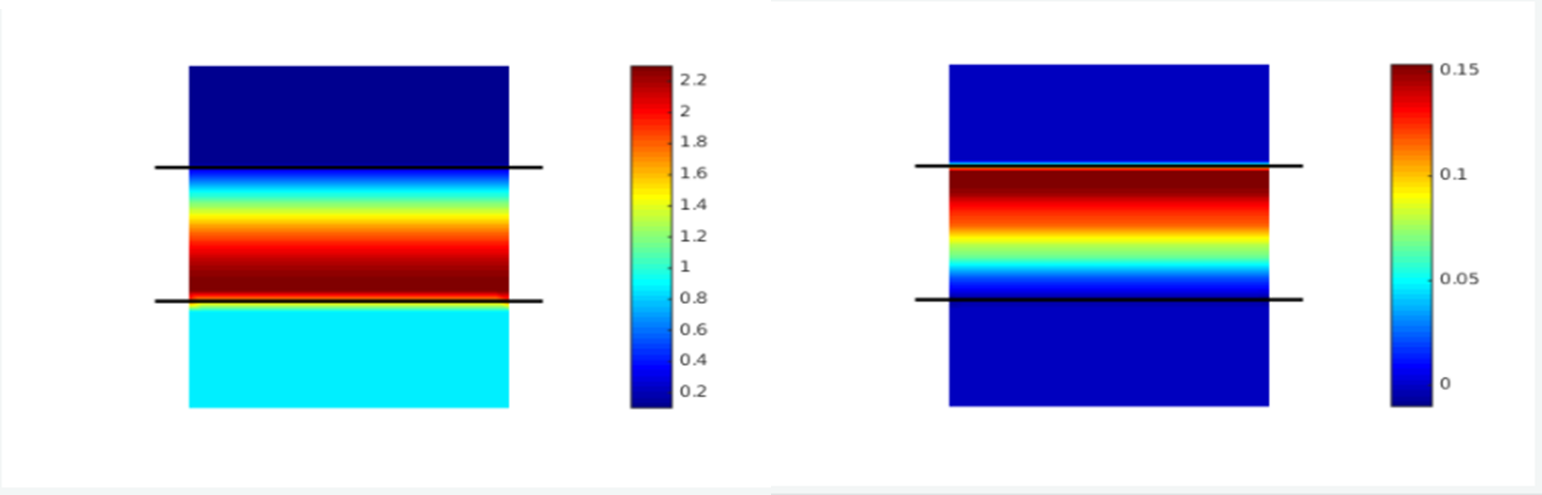
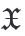
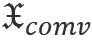 )和密度(例如
)和密度(例如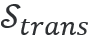 ≈0.9938。通过优化其厚度,可以获得更优异的较低反射性能。
≈0.9938。通过优化其厚度,可以获得更优异的较低反射性能。